Quantum tunneling formula derivation ~ Quantum tunneling also plays a critical role in nuclear fusion electronics and quantum computation. A piezoelectric device that controls the tips elevation in a typical. Indeed lately is being searched by consumers around us, maybe one of you personally. People are now accustomed to using the net in gadgets to view image and video data for inspiration, and according to the name of this post I will talk about about Quantum Tunneling Formula Derivation 9 or 10 gives us.
Source Image @ www.chegg.com
Solved Quantum Tunneling Consider A Finite Rectangular Chegg Com

C C sin θ π 4 displaystyle C_ --Csin left theta - frac pi 4right. A particularly simple example of a state with a current flow is a quantum traveling wave of the form. Your Quantum tunneling formula derivation picture are available in this site. Quantum tunneling formula derivation are a topic that has been searched for and liked by netizens today. You can Download or bookmark the Quantum tunneling formula derivation files here
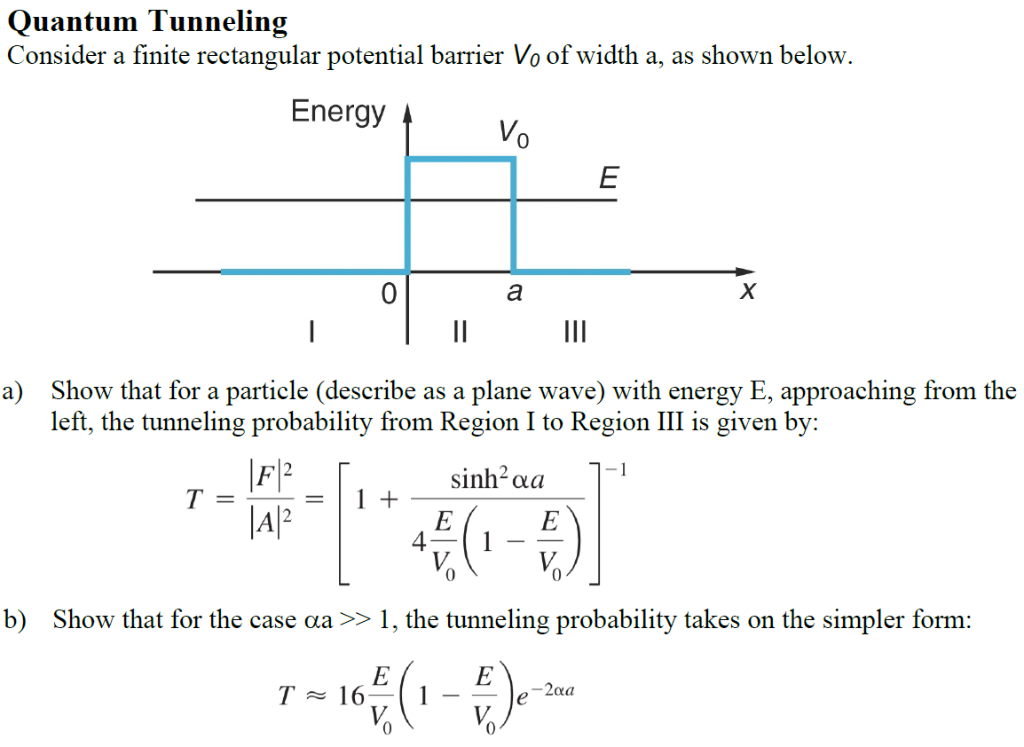
Quantum tunneling formula derivation - Behaviour of a quantum particle at a potential barrier At x0 region I wave function region II wave function. The height of the Coulomb barrier for nuclei of A 200 is about 20-25 MeV. The quantum tunneling phenomenon at metallic surfaces which we have just described is the physical principle behind the operation of the scanning tunneling microscope STM invented in 1981 by Gerd Binnig and Heinrich Rohrer. The phenomenon is interesting and important because it violates the principles of classical mechanics.
Factor out the constant sqrt2mE With the invention of computational online tools one never need to get bogged down in long integrals. Quantum tunneling is a phenomenon in which particles penetrate a potential energy barrier with a height greater than the total energy of the particles. Plug in our integral bound and Vx equation 3 to 4. The derivation is similar to the previous case.
In order to be emitted the alpha particle must penetrate a potential barrier. The time-independent Schrödinger equation must be solved in the three regions and the solutions connected by junction conditions that is the requirement that the wavefunction and its derivative be continuous on. Psi N e-beta x where N is a normalization constant and beta sqrtdfrac2mV-Ehbar2 For a quantum particle to appreciably tunnel through a barrier three conditions must be met Figure PageIndex2. In classical mechanics to describe a system of material points at a certain moment of time it is enough to set every point coordinates and momentum componentsIn quantum mechanics it is in principle impossible to determine simultaneously coordinates and momentum components of even.
Replace C with equation 10 22 to 23. The invention of the tunnel diode in 1957 made it clear. If we follow through the alternative deriva-tion where we wrote the wave function in the form x eifxh and. Combine like terms factor out D and B 23 to 24.
The solution for the Schrödinger equation in such a medium Figure PageIndex2. Derivation of tunneling. Our previous formula for the total transmission coefficient 2 to 3. Quantum tunneling occurs because there exists a nontrivial solution to the Schrödinger equation in a classically forbidden region which corresponds to the exponential decay of the magnitude of the wavefunction.
The Schrödinger equation for the particles wave function is Conditions the wave function must obey are. A particle partially bound within a finite potential well has a certain probability upon each encounter with the barrier of appearing as a free particle on the other side see Figure 1. A Wave Equation for Electrons. The alpha particles emitted in nuclear decay have typical energies of about 5 MeV.
At xL region II wave function region III wave function. Direct substitution of this form into Eq. The STM device consists of a scanning tip a needle usually made of tungsten platinum-iridium or gold. A year later George Gamow used the formalism of quantum mechanics to explain the radioactive alpha-decay of atomic nuclei as a quantum-tunneling phenomenon.
Region 1 Region 2. Since the probability is proportional to the square of the amplitude the approximate tunneling probability is T x10. Alpha decay is a quantum tunneling process. QUANTUM TUNNELING AS A MODEL Quantum mechanics offers an alternative description.
Total Reflection at Boundary. Through a Thin Potential Barrier. O V. At the origin x 0 there is a very high but narrow potential barrier.
A significant tunneling effect can be seen. A Simple Potential Step. The solution for the Schrödinger equation in such a medium Figure PageIndex2. We start with the Schrödinger equation in the form d2 dx 2 p2 h 1 where p p 2mE Vx although this time since E.
This approximate approach to the transmission coefficient through the barrier was used in the introduction to alpha decay which proceeds by quantum mechanical tunneling through the Coulomb barrier and was used to approximate the decay half-life of Polonium. Quantum tunneling refers to the nonzero probability that a particle in quantum mechanics can be measured to be in a state that is forbidden in classical mechanics. The idea of particles tunneling appeared almost simultaneously with quantum mechanics. Psi N e-beta x where N is a normalization constant and beta sqrtdfrac2mV-Ehbar2 For a quantum particle to appreciably tunnel through a barrier three conditions must be met Figure PageIndex2.
In the semiclassical limit we can recover the classical Kramers formula. The Schrödinger Equation Consider an atomic particle with mass m and mechanical energy E in an environment characterized by a potential energy function Ux. This is similar to cluster decay in which an atomic nucleus emits a small cluster of neutrons and protons eg 12 C. T 0 KEY TAKEAWAYS.
Jaa hk m ˆx 11 A Strategy For Solving Tunneling Problems We will limit ourselves to one-dimensional tunneling through a various po-tential barriers. 0008 Expression for ratio AF0720 Complex conjugate AF0820 Value for AAFF0942 Trigonometric identity for cosh²1000 Expression for A². Frustrated Total Reflection Tunneling R 1. Barrier penetration by quantum wave functions was first analyzed theoretically by Friedrich Hund in 1927 shortly after Schrӧdinger published the equation that bears his name.
Quantum tunneling is important in models of the Sun and has a wide range of applications such as the scanning tunneling microscope and the. The quantum tunneling is known to be very sensitive to the barrier shape and energy as shown for example in the context of enzyme catalysis by Hay and coworkers. 0008 Three 3 regions0200 Trial wavefunctions for each of three 3 regions0400 Expressions for k and K0510 Boundary values at x00742 Bounda. The main effect of quantum tunneling is to enhance the reaction kinetics by allowing particles to sometimes tunnel through the barrier from a lower energy rather than diffusing randomly over the top as required by classical statistical mechanics.
This probability is known as the transmis-. Solve for B Equations 25-27 follow the same logic except we are solving for C Now that we have solved for B and C in terms of D we can plug them back into equation 21 to get A_0 in terms of D Remember we want the ratio of DA_0. Thus to assess the importance of QM tunneling we propose an adaptation of definitions of the QM tunneling probability and reaction rate constant based on exact energy levels of the bound system and exact QM tunneling through the. Quantum tunneling through a barrier.
Source Image @ physics.stackexchange.com
Source Image @ hyperphysics.phy-astr.gsu.edu
Source Image @ www.youtube.com
Source Image @ www.mindnetwork.us
Source Image @ www.youtube.com
Source Image @ www.3dincites.com
Source Image @ physicspython.wordpress.com
Source Image @ www.youtube.com
Source Image @ www.quora.com
If you re searching for Quantum Tunneling Formula Derivation you've reached the ideal place. We ve got 10 graphics about quantum tunneling formula derivation including pictures, photos, photographs, wallpapers, and much more. In such webpage, we also have number of images available. Such as png, jpg, animated gifs, pic art, symbol, black and white, transparent, etc.
If the publishing of this web site is beneficial to your suport by discussing article posts of this site to social media marketing accounts you have such as for example Facebook, Instagram among others or can also bookmark this website page with all the title Could An Elementary Particle Do Quantum Tunneling To The Outside Of Spacetime Quora Work with Ctrl + D for computer devices with Glass windows operating system or Command line + D for computer devices with operating system from Apple. If you are using a smartphone, you can even use the drawer menu on the browser you use. Be it a Windows, Macintosh, iOs or Android os operating-system, you'll still be in a position to download images using the download button.

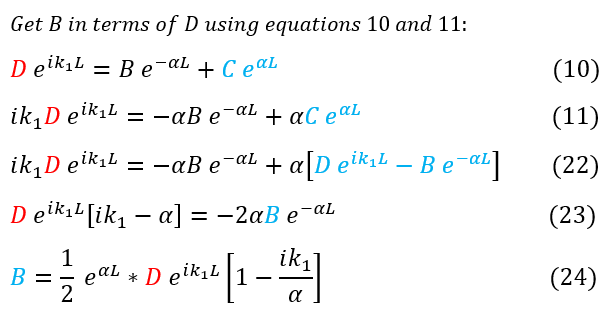




0 comments:
Post a Comment