Quantum harmonic formula ~ I E a t t 0 ℏ Taking into account the QHO wavefunctions. The Quantum Harmonic Oscillator. Indeed recently is being searched by consumers around us, maybe one of you. People are now accustomed to using the internet in gadgets to view video and image data for inspiration, and according to the title of this post I will discuss about Quantum Harmonic Formula In5 Classical harmonic potential for the harmonic oscillator in terms of the reduced mass and frequency is.
Source Image @ slidetodoc.com
Mr Smith Dhs 1617 Simple Harmonic Motion Shm
E n ℏ ω n 1 2 E_n hbar omega leftn frac12right E n ℏ ω n 2 1. The one that we use for essentially all other one-dimensional quantum systems. Your Quantum harmonic formula photographs are ready in this website. Quantum harmonic formula are a topic that has been searched for and liked by netizens today. You can Get or bookmark the Quantum harmonic formula files here
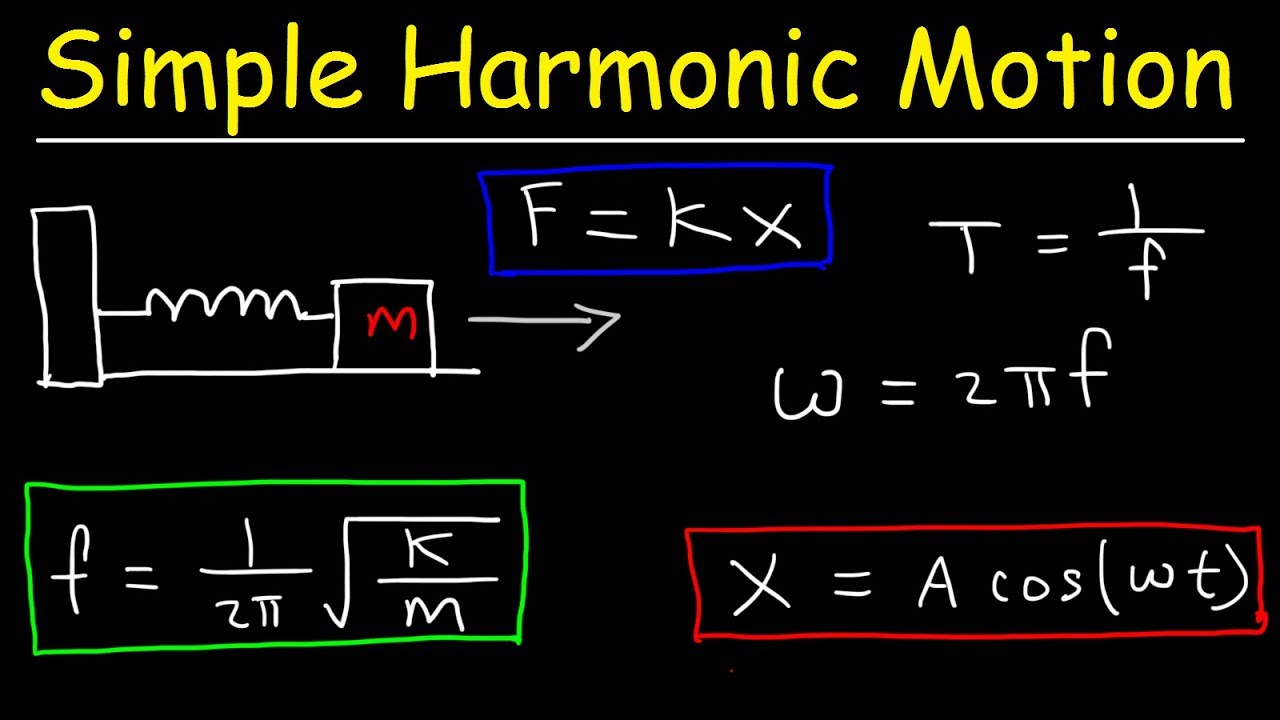
Quantum harmonic formula - Central to this model is the formulation of the quadratic potential energy Vx approx dfrac 12 kx2 labelpotential. It models the behavior of many physical systems such as molecular vibrations or wave packets in quantum optics. The position of the object varies periodically in time with angular frequency. X A.
X t A cos ω t ϕ. This would mean that the green term regardless of if I move in the z direction is a constant. BeginequationE_n left n frac12 right hbar omegaendequation Plugging this expression for energy into the partition function yields. The particle is somewhat localized and cannot escape the potential.
And the normalised harmonic oscillator wave functions are thus ψn π n n xanHxae 2 12 12 xa222 In fact the SHO wave functions shown in the figure above have been normalised in this way. K x t. The quantum harmonic oscillator is a model built in analogy with the model of a classical harmonic oscillator. The Equation for the Quantum Harmonic Oscillator is a second order differential equation that can be solved using a power series.
Schrodinger Equation The Schrodinger equation for a harmonic oscillator may be obtained by using the classical spring potential. M ω π ℏ 1 4 e m ω x 2 2 ℏ H n m ω ℏ x n 0 1 2. 718 where nis the vibrational quantum number and q k. The quantum harmonic oscillator ho.
You can find in Sakurai this expression for the propagator. In following section 22 the power series method is used to derive the wave function and the eigenenergies for the quantum harmonic oscillator. We are now going to consider a system with an infinite number of energy levels. The total energy of the particle is constant.
The natural unit of energy is h. The classical Harmonic Oscillator approximation is a simple yet powerful representation of the energetics of an oscillating spring system. Kharm Out5 2 2x2 ü The Schrødinger equation contains the Hamiltonian which is a sum of the quantum mechanical kinetic energy operator and the quantum mechanical potential energy operator. An harmonic oscillator is a particle subject to a restoring force that is proportional to the displacement of the particle.
The allowed energies of a quantum oscillator are discrete and evenly spaced. Since the derivative of the wavefunction must give back the square of x plus a constant times the original function the following form is suggested. The solutions of the harmonic oscillator Schrödinger equation are. 561 Fall 2017 Lecture 8 Page 4 revised 8717 1121 AM-max.
Students of quantum mechanics will recognize the familiar formula for the energy eigenvalues of the quantum harmonic oscillator. 91 Harmonic Oscillator We have considered up to this moment only systems with a finite number of energy levels. The Hermite equation is a well known to mathematicians differential equation. X A where A denotes the amplitude of the motion.
Show activity on this post. 40 References 1 Lev D. In classical physics this means F. But E ℏ ω n 1 2 so.
We can solve the Schrodinger equation for each wave function using the appropriate boundary conditions. X t a x a a x exp. Is a model that describes systems with a characteristic energy spectrum given by a ladder of. Nu e u2 2 H nu.
In a classic formulation of the problem the particle would not have any energy to be in this region. A wave function in quantum mechanics defined up to an arbitrary constant hence the wave function of a harmonic oscillator can be expressed as following. Once again we emphasize that classical physics predicts total transmission. Z E e β E.
722 Solution of Quantum Harmonic Oscillator With the boundary condition x 0 when x1 it turns out that the harmonic oscillator has energy levels given by E n n 1 2h n 1 2. 5 QUANTUM TUNNELING AND SIMPLE HARMONIC MOTION 2 quantum scale and describe the wave function in terms of an incident wave a reflected wave and a transmitted wave. àClassical harmonic motion The harmonic oscillator is one of the most important model systems in quantum mechanics. In equation 8 if the particle does not move in the x or y directions at all the purple and blue terms are zero.
Note that the energy level are equally spaced and the zero-point energy E 0 1 2. Z n 0 e β ℏ ω 1 2 e β ℏ ω n e β ℏ ω 2 n 0 e β ℏ ω n e β ℏ ω 2 1 1 e β ℏ ω. Roughly speaking there are two sorts of states in quantum mechanics. Equation of motion of harmonic oscillator November 14 2021 January 5 2021 by Editorial staff Harmonic oscillator Equation of motion of harmonic oscillator is fracd2xdt2frackmx0 Frequency of harmonic oscillator is nu frac12pi sqrtfrackm The energy of a harmonic oscillator is E nfrac12hnu.
Second a particle in a quantum harmonic oscillator potential can be found with nonzero probability outside the interval -A leq x leq A. The Schrodinger equation with this form of potential is. The particle can escape the potential. Classical limit of the quantum oscillator A particle in a quantum harmonic oscillator in the ground state has a gaussian wave function.
Quantum Mechanics Non-Relativistic Theory volume III of Course of Theoretical Physics. Divide both sides by psi x psi y psi z. Note that for the same potential whether something is a bound state or an unbound state depends on the energy considered. ω k m ω k m which depends on the mass m of the oscillator and on the force constant k of the net force and can be written as.
C so in conventional units the harmonic oscil-lator energy levels can be summarized in the formula E n n 1 2 h. Quantum Mechanical Harmonic Oscillator Last time. Whereas the energy of the classical harmonic oscillator is allowed to take on any positive value the quantum harmonic oscillator has discrete energy levels E n E_n E n given by. Remember the partition function is.
This answer is not useful. Landau and Evgeny M. A n x 1 2 n n.
Source Image @ hyperphysics.phy-astr.gsu.edu
Source Image @ www.pinterest.co.uk
Source Image @ www.pinterest.com
Source Image @ ibphysics.org
Source Image @ www.youtube.com
Source Image @ slidetodoc.com
Source Image @ hyperphysics.phy-astr.gsu.edu
Source Image @ ibguides.com
Source Image @ byjus.com
If you re looking for Quantum Harmonic Formula you've reached the perfect place. We ve got 10 graphics about quantum harmonic formula adding images, pictures, photos, backgrounds, and much more. In these webpage, we additionally provide number of graphics out there. Such as png, jpg, animated gifs, pic art, logo, black and white, transparent, etc.
If the posting of this site is beneficial to our suport by expressing article posts of this site to social media accounts to have such as for example Facebook, Instagram among others or can also bookmark this website page with the title What Is Simple Harmonic Motion Equation Employ Ctrl + D for laptop or computer devices with House windows operating system or Demand + D for pc devices with operating system from Apple. If you are using a smartphone, you can even utilize the drawer menu of this browser you use. Whether its a Windows, Macintosh personal computer, iOs or Android operating system, you'll be able to download images using the download button.





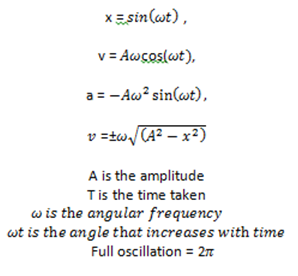

0 comments:
Post a Comment